6. Tableaux▲
6-1. Déclaration▲
Un tableau est un ensemble d'éléments de même type contigus en mémoire.
Pour déclarer un tableau, il est recommandé d'utiliser l'attribut DIMENSION :
TYPE, DIMENSION(expr1,...,exprn) :: liste tabavec :
- kitxmlcodeinlinelatexdvpn \le 7finkitxmlcodeinlinelatexdvp i.e un tableau peut avoir jusqu'à 7 dimensions ;
-
expri sert à indiquer l'étendue dans la dimension correspondante. C'est une expression qui peut être spécifiée à l'aide :
- d'une constante entière (littérale ou symbolique) ; dans ce cas, la borne inférieure du tableau est 1,
- d'une expression de la forme cste1 : cste2 avec cste1, cste2 des constantes entières telles que cste1 <= cste2 ;
- liste_tab est une liste de tableaux.
2.
3.
4.
5.
6.
7.
INTEGER, PARAMETER :: lda = 6
REAL, DIMENSION(0:lda-1) :: Y
REAL, DIMENSION(1+lda*lda,10) :: Z
REAL, DIMENSION(100) :: R
REAL, DIMENSION(1:5,1:5, 1:5) :: S
REAL, DIMENSION(-10:-1) :: X
Remarque : les dimensions d'un tableau peuvent aussi être spécifiées sans l'attribut DIMENSION :
REAL :: T(10,10), U(4,2), G(-1:10,4:9,1:3)Attention, cette notation n'est pas recommandée !
6-2. Définitions (rang, profil, étendue)▲
- Le rang (rank) d'un tableau est son nombre de dimensions.
- Le nombre d'éléments dans une dimension s'appelle l'étendue (extent) du tableau dans cette dimension.
- Le profil (shape) d'un tableau est un vecteur dont chaque élément est l'étendue du tableau dans la dimension correspondante.
- La taille (size) d'un tableau est le produit des éléments du vecteur correspondant à son profil.
- Deux tableaux sont dits conformants s'ils ont le même profil.
2.
REAL, DIMENSION(15) :: X
REAL, DIMENSION(1:5,1:3) :: Y, Z
- Le tableau X est de rang 1, Y et Z sont de rang 2.
- L'étendue de X est 15, Y et Z ont une étendue de 5 et 3.
- Le profil de X est le vecteur (/ 15 /), celui de Y et Z est le vecteur (/ 5,3 /).
- La taille des tableaux X, Y et Z est 15.
- Les tableaux Y et Z sont conformants.
6-2-1. Ordre des éléments▲
En mémoire la notion de tableau n'existe pas : les éléments sont rangés les uns à la suite des autres.
Pour accéder à ces éléments, dans l'ordre mémoire, Fortran fait d'abord varier le premier indice, puis le second et ainsi de suite.
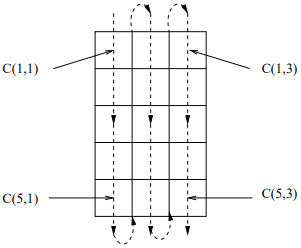
Par exemple, les éléments d'un tableau à deux dimensions sont ordonnés comme suit :
2.
REAL, DIMENSION(5,3) :: C
C(1,1),C(2,1),..,C(5,1),C(1,2),C(2,2),..,C(5,3)
6-3. Initialisation▲
6-3-1. Le symbole « = »▲
Fortran permet de manipuler globalement l'ensemble des éléments d'un tableau.
On pourra alors utiliser le symbole = comme pour l'initialisation d'une variable scalaire.
Exemple : pour initialiser à 3 l'ensemble d'un vecteur :
REAL, DIMENSION(100) :: X = 3.
6-3-2. Le constructeur de vecteurs▲
Un constructeur de vecteur est un vecteur de scalaires dont les valeurs sont encadrées par les caractères (/ et /) :
tableau = (/ expr1, expr2, ..., exprn /)- tableau est un tableau de rang 1 ;
-
expri est :
- le constructeur et le tableau tableau doivent être conformants.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
IMPLICIT NONE
REAL, DIMENSION(4) :: heights = &
(/ 5.10, 5.6, 4.0, 3.6 /)
CHARACTER(len=5), DIMENSION(3) :: colours = &
(/ 'RED ', 'GREEN', 'BLUE ' /)
INTEGER :: i
INTEGER, DIMENSION(10) :: ints = &
(/ 100, (i, i=1,8), 100 /)
6-3-3. L'instruction DATA▲
Comme pour les variables simples, on peut utiliser l'instruction DATA pour initialiser les tableaux lors de leur déclaration. Elle permet d'initialiser tout ou partie de tableaux à l'aide d'une liste de constantes encadrée par le caractère / (la notation n*valeur peut être employée pour répéter une même valeur).
Les éléments à initialiser peuvent être spécifiés au moyen d'une boucle DO implicite : (tab(i), i = m1,m2[,m3]).
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
IMPLICIT NONE
INTEGER :: i, j
REAL, DIMENSION(20) :: A, B
INTEGER, DIMENSION(10) :: ints
REAL, DIMENSION(2,3) :: MAT
DATA A/20*7.0/, B/10., 3.87, 10.5/
DATA (ints(i),i=1,4)/4*6.0/, A(10)/-1.0/
DATA MAT/1., 2., 3., 4., 5., 6./
DATA ((MAT(i,j),j=1,3),i=1,2)/1., 2., 3., &
4., 5., 6./
6-4. Manipulation de tableaux▲
6-4-1. Expressions de type tableau▲
Les tableaux peuvent être utilisés en tant qu'opérandes dans une expression :
- les opérateurs intrinsèques sont applicables à des tableaux conformants ;
- les fonctions élémentaires s'appliquent à l'ensemble du tableau.
Dans ces cas, les fonctions ou opérateurs sont appliqués à chaque élément du tableau (log, sqrt…).
2.
3.
4.
5.
6.
REAL, DIMENSION(-4:0,0:2) :: B
REAL, DIMENSION(5,3) :: C
REAL, DIMENSION(0:4,0:2) :: D
...
B = C * D - B**2
B = SIN(C)+COS(D)
6-4-2. Sections de tableaux▲
Les sections régulières de tableaux sont décrites à l'aide d'un triplet :
[limite1]:[limite2][:pas]- cette notation est équivalente à une pseudoboucle ;
- une section de tableau est aussi un tableau ;
- le rang d'une section de tableau est inférieur ou égal à celui du tableau global ;
- la section démarre à limite1 et se termine à ou avant limite2 ;
- pas est l'incrément des indices.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
A(:) ! Le tableau global
A(3:9) ! A(3) à A(9) par pas de 1
A(3:9:1) ! Idem
A(m:n) ! A(m) à A(n)
A(m:n:k) ! A(m) à A(n) par pas de k
A(8:3:-1) ! A(8) à A(3) par pas de -1
A(8:3) ! A(8) à A(3), pas de 1 => taille nulle
A(m:) ! de A(m) à la borne supérieure de A
A(:n) ! de la borne inférieure de A à A(n)
A(::2) ! borne inf. de A à borne sup., pas de 2
A(m:m) ! section constituée de 1 élément
! (ce n'est pas un scalaire !)
A(m) ! section équivalente à un scalaire
Seules les opérations sur des sections conformantes sont valides :
2.
3.
4.
5.
REAL, DIMENSION(1:6,1:8) :: P
P(1:3,1:4) = P(1:6:2,1:8:2) ! VALIDE
P(2:8:2,1:7:3) = P(1:3,1:4) ! INVALIDE
P(2:6:2,1:7:3) = P(2:5,7) ! INVALIDE
Exemples
REAL, DIMENSION(1:6,1:8) :: P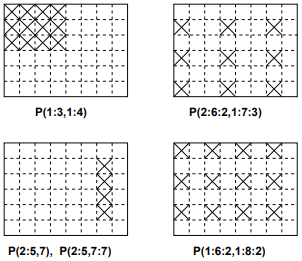
Attention, P(2:5,7) est une section 1D tandis que P(2:5,7:7) est une section 2D : ces 2 tableaux ne sont donc pas conformants.


